Rozwój matematyki: system dedukcyjny, teoria mnogości

Rozwój matematyki zaczął się od arytmetyki, algebry i geometrii. Nic też dziwnego, że początkowo matematyka była określana jako nauka o liczbach i figurach geometrycznych.
Matematyka należy do najstarszych nauk, których korzenie sięgają starożytnego Egiptu oraz Mezopotamii. Jako odrębna nauka ukształtowała się w Grecji w IV w. p.n.e. Wtedy to Euklides stworzył pierwszy system dedukcyjny zwany geometrią euklidesową.
System dedukcyjny
System dedukcyjny to taki zbiór twierdzeń, w którym z twierdzeń wyjściowych zwanych aksjomatami lub postulatami wyprowadza się w sposób logicznie niezawodny wszystkie dalsze twierdzenia zwane tezami systemu.
W całej swej 25-wiekowej historii matematyka nigdy nie była nauką tak żywotną jak obecnie. Wcześniej, najbardziej rozwijała się u swych początków w starożytnej Grecji. Następnie w XIX-wiecznej Europie. Natomiast niemal nie istniała jako nauka w starożytnym Rzymie ani w Ameryce przed 1870 r.
Obecnie, z uwagi na ogromny rozrost matematyki, nie udaje się adekwatnie podać w sposób wyczerpujący przedmiotu jej badań. Nie jest to tylko nauka o liczbach, czy wielkościach – potrafi ona w sposób ścisły ujmować także jakościowe aspekty zjawisk.
Można by ogólnie powiedzieć, że jest to nauka dedukcyjna i formalna (tzn. nie odwołująca się w toku uzasadniania swych twierdzeń do doświadczenia) o rozmaitych abstrakcyjnych strukturach, złożonych z liczb, figur geometrycznych, zbiorów, grup, funkcji, kategorii itp.
Poszczególne teorie matematyczne to zbiory twierdzeń (tez), które dają się wydedukować (wyprowadzić) za pomocą reguł wnioskowania z przyjętego układu aksjomatów. Niemiecki matematyk i filozof matematyki Gottlob Frege (profesor Uniwersytetu Jenajskiego) oraz włoski matematyk i logik Giuseppe Peano (profesor Uniwersytetu w Turynie) pierwsi zaczęli ujmować matematykę w XIX w. jako zbiór aksjomatycznych systemów dedukcji.
Teoria mnogości
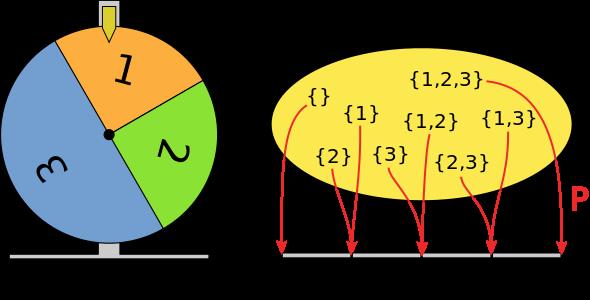
Druga połowa XIX w. była okresem wielkiego przełomu zarówno w matematyce, jak i w logice. W matematyce dokonał się on za sprawą utworzenia przez matematyka niemieckiego Georga Cantora (profesor Uniwersytetu w Halle) teorii mnogości, stanowiącej teorię zbiorów, która największy wkład wniosła do zrozumienia zbiorów nieskończonych. Dlatego jądrem teorii mnogości, tworzącym najbardziej oryginalną jej część, jest teoria liczb pozaskończonych. Według Davida Hilberta jest ona najbardziej godnym podziwu tworem ducha matematycznego i w ogóle jednym z największych osiągnięć intelektu ludzkiego.

Zasadnicze znaczenie miało udowodnienie przez Georga Cantora i Juliusa Richarda Dedekinda (profesor Wyższej Szkoły Technicznej w Brunszwiku), że wiele twierdzeń słusznych dla zbiorów skończonych, np. że część jest mniejsza od całości, że istnieje minimum i maksimum, że zachodzi przemienność ciągu składników czy czynników, nie znajduje zastosowania w odniesieniu do zbiorów nieskończonych, które – na mocy definicji – okazują się równoliczne z niektórymi ze swoich podzbiorów właściwych (np. zbiór liczb naturalnych ma tyle samo elementów co zbiór liczb parzystych).
Można powiedzieć za Hilbertem, że dzięki gigantycznej pracy Fregego, Dedekinda oraz Cantora, „nieskończoność została posadzona na tronie”. G. Frege i R. Dedekind, jako pierwsi posługiwali się pojęciem nie tylko potencjalnej lecz także aktualnej nieskończoności w matematyce.
Rozwój matematyki umożliwia rozwój fizyki
W ogóle należy podkreślić, że dalszy rozwój fizyki – zwłaszcza fizyki teoretycznej – jest niemożliwy bez rozwoju matematyki. Mogą o tym najdobitniej świadczyć trudności matematyczne na jakie natknęła się teoria superstrun.
Tak było też dotąd. Na przykład bez rachunku tensorowego, którego podstawy opracowali (w 1900 r.) włoscy matematycy Gregorio Ricci-Curbastro (od 1880 r. prof. uniw. w Padwie) oraz jego uczeń Tulio Levi Civita (od 1902 r. prof. uniw. w Padwie), nie mogłaby powstać OTW (ogólna teoria względności). Natomiast bez przestrzeni Banacha (największego polskiego matematyka) oraz „nadbudowanej” nad nią przestrzeni Hilberta (najwybitniejszego współczesnego matematyka niemieckiego), nie mogłaby powstać mechanika kwantowa.
Synergetyka i cybernetyka
Synergetyka posiada interdyscyplinarny (wykraczający poza czystą matematykę) charakter. Określana jest mianem teorii samoorganizacji. Opiera się ona na założeniu, że współpraca wielu podsystemów jakiegokolwiek systemu jest podporządkowana tym samym prawom, niezależnie od natury elementów.
 Najważniejszą zaś dyscypliną interdyscyplinarną, wyrosłą na podstawie matematyki, fizyki oraz wielu innych nauk jest cybernetyka. Jest to nauka o sterowaniu i łączności w żywych organizmach i maszynach. Jej głównym twórcą jest wprawdzie matematyk amerykański Norbert Wiener, ale ma ona licznych wybitnych przedstawicieli także w Europie. Jednym z najwybitniejszych jest matematyk rosyjski Andriej Kołmogorow.
Najważniejszą zaś dyscypliną interdyscyplinarną, wyrosłą na podstawie matematyki, fizyki oraz wielu innych nauk jest cybernetyka. Jest to nauka o sterowaniu i łączności w żywych organizmach i maszynach. Jej głównym twórcą jest wprawdzie matematyk amerykański Norbert Wiener, ale ma ona licznych wybitnych przedstawicieli także w Europie. Jednym z najwybitniejszych jest matematyk rosyjski Andriej Kołmogorow.
Ilustracje
Euklides – źródło: Wikimedia Commons
Georg Cantor – źródło: Wikimedia Commons