Matematyka
-
Polska Szkoła Matematyczna
Polska Szkoła Matematyczna, która uzyskała rozgłos światowy, zaczęła się kształtować na uniwersytetach w Krakowie i Lwowie jeszcze przed II wojną światową. Jej zalążek stanowiła grupa matematyków utworzona w roku 1911 we Lwowie przez Wacława Sierpińskiego (od 1910 prof. Uniw. Lwowskiego, od 1919 prof. Uniw. Warszawskiego), do której należeli także Zygmunt Janiszewski (od 1918 r. iprof. Uniw. Warszawskiego) i Stefan Mazurkiewicz (od 1919 r. prof. Uniw. Warszawskiego). Początki Polskiej Szkoły Matematycznej W r. 1917 Janiszewski opublikował artykuł programowy O potrzebach matematyki w Polsce, Postulował w nim, aby skupić aktywnych badaczy na jednym powstałym niedawno obszarze matematyki (chodziło o teorię mnogości), jak też założenie czasopisma poświęconego tej tematyce oraz publikującego wyłącznie w…
-
Dyscypliny matematyki
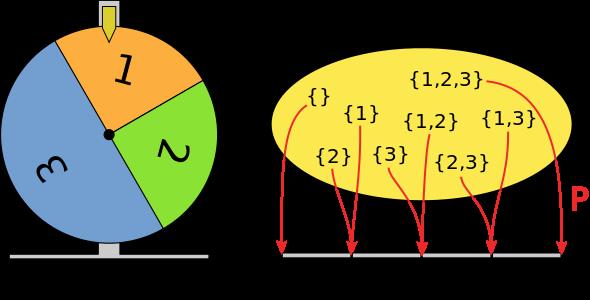
Dyscypliny matematyki, to współcześnie bardzo szeroki temat, dlatego omówię tylko niektóre. Ważną dyscypliną matematyki współczesnej jest – obok algebry, topologii, geometrii, logiki – analiza. David Hilbert nazwał ją kiedyś (w 1926 r.) „najkunsztowniej i najpiękniej rozgałęzioną budowlą matematyczną”. Rachunek prawdopodobieństwa natomiast jest istotny, zwłaszcza w zastosowaniach. Rachunek prawdopodobieństwa Początki jego sięgają XVII stulecia, kiedy to doczekał się pierwszego opracowania (po wcześniejszych już opisach). Dokonali tego Pierre Fermat oraz Blaise Pascal. Po kolejnych pracach w następnych wiekach, duży wkład w rozwój teorii prawdopodobieństwa wniósł matematyk rosyjski Andriej Kołmogorow, który dokonał pełnej aksjomatyzacji rachunku w latach trzydziestych XX wieku. W otoczeniu Kołmogorowa pracowało wielu matematyków, m.in. Aleksander Chińczyn, który metody prawdopodobieństwa zastosował do…
-
Matematyka niestandardowa
Matematyka niestandardowa (w tym niestandardowa analiza matematyczna oraz niestandardowa teoria mnogości) utworzona została w 1960 roku przez Abrahama Robinsona. Zwana też analizą niestandardową jest działem matematyki. Przewiduje się, że może ona nabrać decydującego znaczenia dla dalszego rozwoju fizyki. Niestandardowa analiza matematyczna Robinson opracował nowe ujęcie klasycznej analizy matematycznej, nazwane przez niego „analizą niestandardową”. Pozwoliła ona na ścisłe i logicznie bez zarzutu zdefiniowanie takich pojęć, jak wielkości nieskończenie małe i nieskończenie duże. Pojęciami tymi posługiwali się też Gottfried Leibniz oraz Izaak Newton, jako twórcy rachunku różniczkowego oraz całkowego. Abraham Robinson (1918–1974), to matematyk żydowskiego pochodzenia, od lat sześćdziesiątych przebywający w Ameryce. Zajmował się też matematyką stosowaną, analizą, algebrą oraz logiką matematyczną. Wniósł też…
-
Podstawy matematyki: David Hilbert, Kurt Gödel
David Hilbert w fundamentalnym dziele Podstawy geometrii (1899 r.) podał pełną aksjomatykę geometrii Euklidesa. Pokazał jednocześnie, że system samego Euklidesa (wyłożony w jego Elementach) zawierał cały szereg założeń ukrytych (implicite), nie sformułowanych dotąd ani przez samego twórcę, ani przez jego następców. Metamatematyka Podobnie Richard Dedekind oraz Giuseppe Peano dokonali aksjomatyzacji arytmetyki liczb naturalnych. Zasługą Hilberta jest też stworzenie nowego działu matematyki zwanego metamatematyką. Jest to nauka o podstawach matematyki. Można ją też nazwać nauką o matematyce. Zajmuje się ona badaniem systemów dedukcyjnych. Hilbert określił ją jako naukę o dowodzeniu matematycznym (jako teorię dowodów sformalizowanych), a samą matematykę nazwał systemem formuł dowodliwych. David Hilbert jest też twórcą pojęcia przestrzeni Hilberta. Przestrzeń…
-
Rozwój matematyki: system dedukcyjny, teoria mnogości
Rozwój matematyki zaczął się od arytmetyki, algebry i geometrii. Nic też dziwnego, że początkowo matematyka była określana jako nauka o liczbach i figurach geometrycznych. Matematyka należy do najstarszych nauk, których korzenie sięgają starożytnego Egiptu oraz Mezopotamii. Jako odrębna nauka ukształtowała się w Grecji w IV w. p.n.e. Wtedy to Euklides stworzył pierwszy system dedukcyjny zwany geometrią euklidesową. System dedukcyjny System dedukcyjny to taki zbiór twierdzeń, w którym z twierdzeń wyjściowych zwanych aksjomatami lub postulatami wyprowadza się w sposób logicznie niezawodny wszystkie dalsze twierdzenia zwane tezami systemu. W całej swej 25-wiekowej historii matematyka nigdy nie była nauką tak żywotną jak obecnie. Wcześniej, najbardziej rozwijała się u swych początków w starożytnej Grecji. Następnie w…