Ogólna teoria względności (OTW)

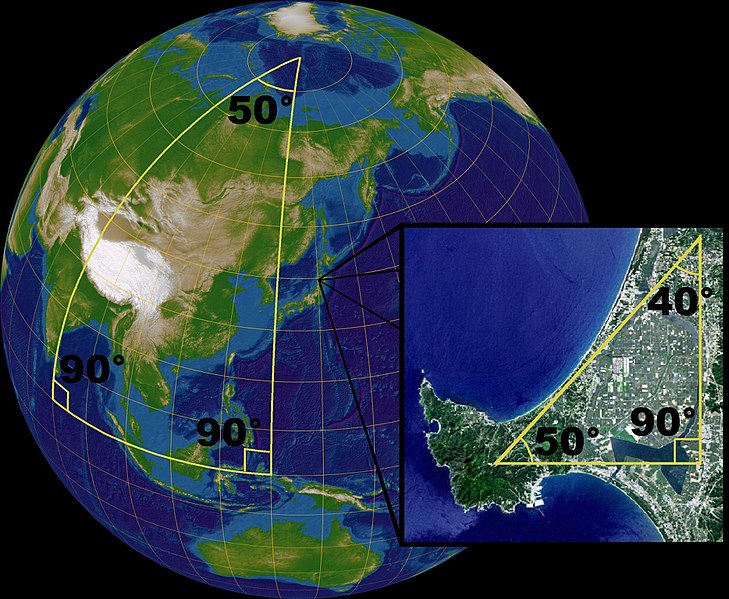
Obrazek: Trójkąt Riemanna na sferze oraz trójkąt Euklidesa na płaszczyźnie

Ogólna teoria względności (OTW), opracowana przez Alberta Einsteina w 1915 r., ustaliła nowe fundamentalne własności czasu i przestrzeni (czasoprzestrzeni). Główną z nich jest zależność czasu i przestrzeni od rozkładu i gęstości materii: w pobliżu wielkich mas czasoprzestrzeń jest zakrzywiona dodatnio, czyli jest czasoprzestrzenią Riemanna.

Zamiast: zakrzywienie czasoprzestrzeni można też mówić: krzywizna czasoprzestrzeni.

­

Czasoprzestrzeń Bernharda Riemanna różni się od czasoprzestrzeni Hermanna Minkowskiego tym, że czasoprzestrzeń Minkowskiego jest

• płaska, niezakrzywiona, euklidesowa (ściślej mówiąc jest “pseudoeuklidesowa”, prawie euklidesowa, gdyż współrzędne przestrzenne występują w niej ze znakiem +, natomiast przestrzenna czasowa – ze znakiem –);

a czasoprzestrzeń Riemanna jest

• zakrzywiona, nieeuklidesowa.

Zakrzywienie czasoprzestrzeni może być dodatnie lub ujemne. W związku z tym geometria nieeuklidesowa występuje w dwóch odmianach:

• jako geometria Łobaczewskiego, która opisuje czasoprzestrzeń o ujemnym zakrzywieniu oraz
• geometria Riemanna, opisująca czasoprzestrzeń o zakrzywieniu dodatnim.

Dla jasności należy oddzielnie omówić pojęcie zakrzywienia przestrzeni oraz pojęcie zakrzywienia czasu.  

 

Jeśli chodzi o pojęcie zakrzywienia przestrzeni to można je rozpatrywać w dwóch ujęciach, jako:

(1) pojęcie matematyczne

(2) pojęcie fizyczne

W matematyce opracowano 3 rodzaje geometrii:

• Geometria Łobaczewskiego
  K = – ;   suma kątów trójkąta jest mniejsza od 180°;    πŁ > πE

• Geometria Euklidesa
  K = 0;   suma kątów trójkąta = 180°;   πE = 3,14159…

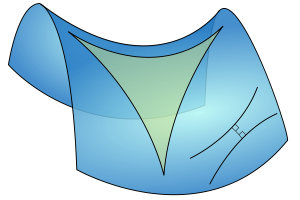
• Geometria Riemanna
  K = +;  suma kątów trójkąta jest większa od 180°; πR < πE

iK = – oznacza, że przestrzeń jest zakrzywiona ujemnie
lK = 0 oznacza, że przestrzeń jest płaska, niezakrzywiona
IK = + oznacza, że przestrzeń jest zakrzywiona dodatnio
π – liczba “Pi“, Ł – Łobaczewskiego, E – Euklidesa, R – Riemanna

Obrazowo różnice między trzema rodzajami przestrzeni można zobrazować za pomocą poszczególnych figur geometrycznych, takich jak trójkąt lub koło.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

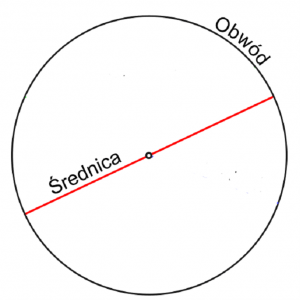
πE =  3,141592…       π  – stosunek obwodu koła do średnicy

Zakrzywienie czasoprzestrzeni w sensie matematycznym to odstępstwo od geometrii Euklidesa:

• ­geometria Euklidesa = geometria przestrzeni niezakrzywionej (płaskiej)
• ­geometria nieeuklidesowa = geometria przestrzeni zakrzywionej (dodatnio lub ujemnie).

(2) Zakrzywienie przestrzeni w sensie fizycznym

Albert Einstein w 1907 r. doszedł do wniosku, że przestrzeń fizyczna jest zakrzywiona dodatnio, czyli jest przestrzenią Riemanna.

Przestrzeń jest płaska (euklidesowa, niezakrzywiona) w sensie fizycznym, jeśli ciało w stanie swobodnym (tzn. ciało, na które nie działają żadne siły) porusza się w niej jednostajnie i prostoliniowo, czyli inercyjnie, bez przyśpieszenia w szerokim sensie fizycznym (tzn. nie zmienia prędkości ani kierunku).

­

Natomiast przestrzeń jest zakrzywiona (nieeuklidesowa) w sensie fizycznym, jeśli ciało w stanie swobodnym porusza się w niej nieinercyjnie, czyli z przyśpieszeniem, co do prędkości lub kierunku: Jeśli przyśpieszenie ciała w stanie swobodnym jest dośrodkowe (tzn. odbywa się w kierunku do grawitującej masy), to przestrzeń jest zakrzywiona dodatnio, czyli jest przestrzenią Riemanna. Jeśli natomiast przyśpieszenie ciała w stanie swobodnym jest odśrodkowe (tzn. odbywa się w kierunku od grawitującej masy), to przestrzeń jest zakrzywiona ujemnie, czyli jest przestrzenią Łobaczewskiego.

­W 1919 roku w czasie zaćmienia Słońca obserwacja astronomiczna potwierdziła OTW:

promienie biegnące od gwiazd w pobliżu Słońca biegły po torach zakrzywionych w kierunku Słońca, co wskazywało na to, że Słońce zakrzywia przestrzeń dodatnio (po Riemannowsku).

Grawitacja według OTW nie jest siłą działającą na odległość, lecz zakrzywieniem czasoprzestrzeni.

Na czym polega zakrzywienie czasu?

Odpowiadając na to pytanie muszę się ograniczyć do stwierdzenia, że zakrzywienie czasu objawia się w spowolnieniu czasu, które jest zależne od rozkładu i gęstości materii. Oznacza to, że w pobliżu wielkich mas czas jest zakrzywiony, czyli płynie wolniej, niż z dala od mas.

Spowolnienie czasu w danym obiekcie wskazuje, że wszystkie procesy zachodzące w tym obiekcie przebiegają wolniej. Dla obiektów żywych oznacza to, że także  proces starzenia przebiega wolniej, co prowadzi do paradoksów, omówionych w poprzednim wpisie.

W fizyce relatywistycznej (STW i OTW) występują dwie dylatacje czasu:

(1) w STW: im ciało porusza się szybciej, tym czas w nim płynie wolniej;
(2) w OTW: im ciało znajduje się bliżej wielkiej masy, tym czas w nim płynie wolniej.

Ilustracje

Trójkąt Riemanna oraz Euklidesa – źródło: Wikimedia Commons 
Albert Einstein ze swoją pierwszą żoną Milevą Maric – źródło: Wikimedia Commons
Euklides – źródło: Wikimedia Commons  
Trójkąt Łobaczewskiego – źródło: Wikimedia Commons  
Nikołaj Łobaczewski– źródło: Wikimedia Commons
Bernhard Riemann – źródło: Wikimedia Commons

Zob. też: Szczególna teoria względności