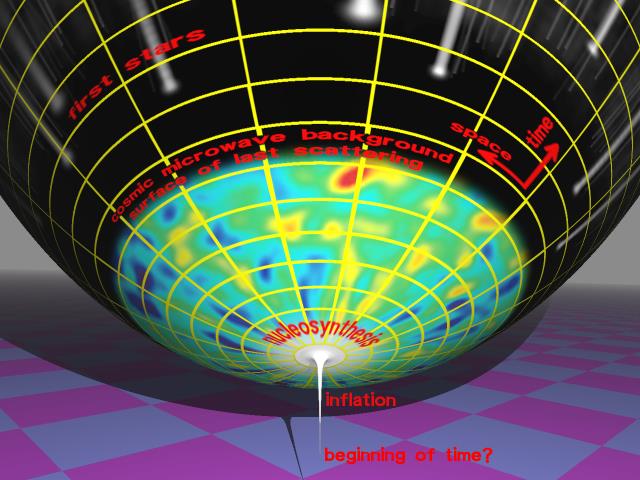
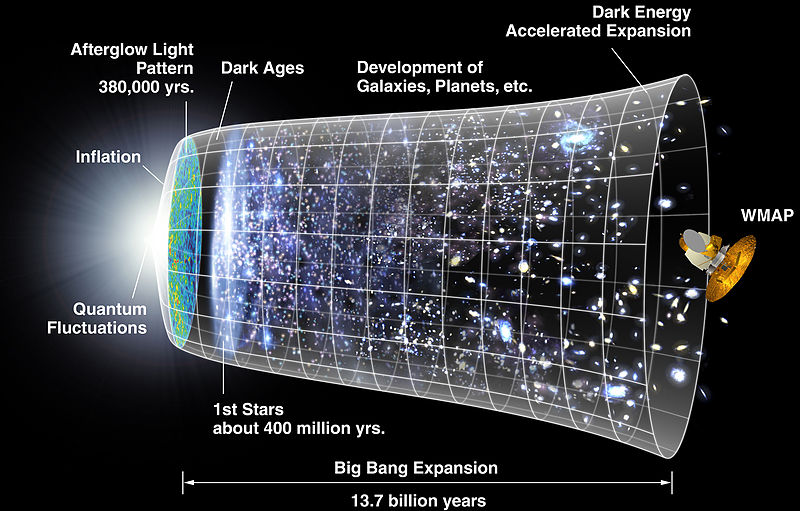
Problemy nieskończoności świata (1)

Z tematu Problemy nieskończoności świata omówię (w tym wpisie) następujące zagadnienia:

1. Ilościowe i jakościowe problemy nieskończoności świata
2. Problemy nieskończoności Wszechświata związane z  czasem i przestrzenią
3. Problem materialnej i przestrzennej nieskończoności Wszechświata:
   • a. stanowisko starożytnych
   • b. stanowisko nauki nowożytnej (1600 r.–1900 r.)
   • c. stanowisko nauki współczesnej (XX w.)

oraz zagadnienia:

1. Nieskończoność a nieograniczoność materialna i  przestrzenna Wszechświata
2. Problem genetycznej i czasowej nieskończoności Wszechświata
3. Nieskończoność a nieograniczoność genetyczna i czasowa Wszechświata
4. Problemy nieograniczoności Wszechświata
5. Problem wieczności Wszechświata

w następnym wpisie, pod nazwą Czy świat jest nieskończony?

1. Ilościowe i jakościowe problemy nieskończoności świata

Problemy nieskończoności Wszechświata podejmuje filozofia i kosmologia. Można podzielić je na problemy ilościowe i jakościowe.

Przykłady problemów ilościowych:

• czy ilość materii jest nieskończona?
• czy czas jest nieskończony?
• oraz, czy przestrzeń jest nieskończona?

Przykłady problemów jakościowych:

• czy ilość rodzajów materii jest nieskończona?
• czy ilość rodzajów ruchu jest nieskończona?
• ale też, czy ilość praw rządzących Wszechświatem jest nieskończona?

2. Problemy nieskończoności Wszechświata związane z czasem i przestrzenią

W problemach nieskończoności Wszechświata związanych z czasem i przestrzenią trzeba wyróżnić

8 problemów: 

• a. 4 problemy kosmologiczne
• b. 4 problemy mikrofizyczne

a. Cztery problemy kosmologiczne, tj. problemy nieskończoności „wszerz”

(1) Problem nieskończoności czasowej Wszechświata:

  czy czas jest nieskończony?

W sformułowaniu ścisłym, ilościowym: czy czas trwa nieskończoną ilość jednostek czasowych, np. sekund czy lat. Jeśli czas trwa nieskończoną ilość jednostek, to mówimy, że czas jest nieskończony.

(2) Problem nieskończoności genetycznej Wszechświata:

czy świat trwa skończoną czy nieskończoną ilość jednostek czasu, np. sekund czy lat.

Różnica między tymi dwoma problemami jest wyraźnie widoczna w modelu Wszechświata Tomasza z Akwinu, zgodnie z którym Wszechświat został stworzony przez Boga w pewnym momencie czasu i kiedyś przestanie istnieć. Zgodnie z tym modelem sam czas jest nieskończony, ale świat jest skończony w czasie, czyli genetycznie skończony.

(3) Problem nieskończoności przestrzennej Wszechświata:

czy przestrzeń jest nieskończona, tzn. czy przestrzeń ciągnie się w nieskończoność w dowolnym kierunku, czy też nie?

W sformułowaniu ilościowym: czy przestrzeń Wszechświata zawiera w sobie skończoną czy nieskończoną ilość jednostek przestrzennych, np. cm³, czy km³.

(4) Problem materialnej nieskończoności Wszechświata, który można sformułować w dwóch wersjach:

• a) czy materia zajmuje skończony czy nieskończony obszar przestrzenny (czy materia ciągnie się w nieskończoność w dowolnym kierunku przestrzennym?);
• b) czy ilość materii (mierzona w jednostkach masy: gram, kg, tona) jest nieskończona?

Obie te wersje a) i b) są równoważne przy założeniu, że gęstość materii jest wszędzie skończona, tzn. że nie jest ani nieskończenie mała, ani nieskończenie duża.

Dla odróżnienia problemu (3) i (4) można się posłużyć modelem średniowiecznych Arabów, którzy głosili, że materia jest tylko skończoną wysepką w oceanie nieskończonej przestrzeni.

Problemy (1) i (2) są równoważne przy założeniu, że nie ma pustego czasu, natomiast problemy (3) i (4) są równoważne przy założeniu, że nie ma pustej przestrzeni.

Prawdziwość tych założeń sprawia, że cztery te problemy redukują się do dwóch.

b. Cztery problemy mikrofizyczne (mikrokosmiczne), tj. nieskończoności „w głąb”

Dotyczą one nieskończonej podzielności materii, czasu i przestrzeni. Są to:

(5) Problem nieskończonej podzielności czasu:

czy czas jest nieskończenie podzielny?

Fizycy nazywają go problemem kwantyzacji czasu: czy czas składa się z kwantów czasu – jednostek, których już nie można dalej dzielić.

W języku matematycznym jest to pytanie: czy czas jest zbiorem ciągłym (zwanym continuum), czy też zbiorem dyskretnym.

Dawniej, na płaszczyźnie mechaniki kwantowej, sądzono, że kwant czasu zwany chronomem wynosi: 1ch = 10^–24 sek, jednakże współcześnie budowane teorie fizyczne sugerują, że kwant czasu = 10^–44 sek – jest to tzw. czas Plancka.

(6) Problem nieskończonej podzielności materii w aspekcie czasowym:

czy istnieją najkrótsze procesy – procesy elementarne, dalej niepodzielne? Proces elementarny trwałby jeden kwant czasu.

(7) Problem nieskończonej podzielności przestrzeni:

czy przestrzeń jest nieskończenie podzielna?

Fizycy nazywają go problemem kwantyzacji przestrzeni i łączą go z problemem kwantyzacji czasu. Mamy zatem problem fizyczny kwantyzacji czasu i przestrzeni. Na płaszczyźnie mechaniki kwantowej sądzono, że kwantem przestrzeni (długości) jest pewna elementarna długość, która wynosi 1 fermi = 10^–13 cm. Współczesne teorie fizyczne sugerują, że elementarną długością jest długość Plancka = 10^–33 cm.

Kwant czasu i przestrzeni wiąże stała prędkość światła C:

 

• kwant przestrzeni to odległość, jaką przebywa światło w okresie jednego kwantu czasu,
• a kwant czasu jest to czas jaki potrzebuje światło do przebycia kwantu przestrzeni.

 

(8) Problem nieskończonej podzielności materii w aspekcie przestrzennym:

czy istnieją najmniejsze obiekty (cząstki) materii (czy istnieją atomy Demokryta), dalej niepodzielne? (Jest to problem postawiony przez Demokryta).

W fizyce współczesnej problem ten można sformułować w pytaniu:

  czy istnieją cząstki „absolutnie elementarne”, tzn. cząstki pozbawione jakiejkolwiek struktury wewnętrznej, bezwzględnie proste (pozbawione wewnętrznych stopni swobody)?

3. Problem materialnej i przestrzennej nieskończoności Wszechświata

a) stanowisko starożytnych

Problem ten łączy dwa problemy: problem nieskończoności materialnej oraz nieskończoności przestrzennej Wszechświata.

Starożytni opracowali dwa modele Wszechświata:

• model przednaukowy (mitologiczny)
• oraz model naukowy.

Model mitologiczny zakładał, że Ziemia jest płaska i przedstawiał Wszechświat w kształcie półkuli, od góry ograniczonej przez gwiazdy, od dołu przez Ziemię i wodę.

W ramach tego modelu istniały trzy poglądy:

• (1) pierwszy, że Wszechświat jest materialnie i przestrzennie skończony;
• (2) drugi, że jest materialnie skończony a przestrzennie nieskończony oraz
• (3) trzeci, że jest nieskończony zarówno materialnie jak i przestrzennie.

(3) Trzeci pogląd reprezentował Anaksymander (apeiron bez granic) oraz atomiści. Według Demokryta ilość atomów jest nieskończona i zajmują one nieskończony obszar przestrzenny

Według (2) drugiego modelu – naukowego, opracowanego przez Arystotelesa i Ptolemeusza, Ziemia jest kulista i znajduje się w środku kulistego Wszechświata.

Arystoteles wyróżnił we Wszechświecie dwa obszary:

• ziemski (podksiężycowy)
• i niebieski, który się ciągnie od sfery księżyca do sfery gwiazd.

Poza sferą gwiazd nie istnieje nic, nie ma nawet pustej przestrzeni.

Także w ramach tego modelu ukształtowały się trzy poglądy:

• (a) pogląd Arystotelesa i Ptolemeusza, że Wszechświat jest materialnie i przestrzennie skończony,
• (b) pogląd, że jest materialnie skończony lecz przestrzennie nieskończony oraz
• (c) pogląd atomistów, że jest materialnie i przestrzennie nieskończony.

Pogląd (b) i (c) był podtrzymywany przez geometrię Euklidesa, zgodnie z którą linie proste, płaszczyzny i trójwymiarowa przestrzeń mogą się ciągnąć w nieskończoność. Ogólnie wśród starożytnych Greków zdecydowanie dominował pogląd, że świat jest materialnie i przestrzennie skończony.

Także Mikołaj Kopernik, budując swój model heliocentryczny (gr. helios – słońce), skłaniał się do wniosku, że Wszechświat jest materialnie i przestrzennie skończony. Tyle tylko, że w środku znajduje się nie Ziemia (jak głosił model geocentryczny Ptolemeusza) lecz Słońce. Pod tym względem Kopernik raczej zamknął starą epokę, niż otworzył nową. Tym niemniej, Kopernik przyczynił się do zwycięstwa w nauce nowożytnej koncepcji Wszechświata materialnie i przestrzennie nieskończonego.

b) stanowisko nauki nowożytnej   (1600–1900 r.)

Czwarty model Wszechświata, odpowiadający w pełni czasom nowożytnym, opracował Giordano Bruno, który zmodyfikował heliocentryczny model Kopernika. Według Bruno Wszechświat jest materialnie i przestrzennie nieskończony. Jako taki nie ma ani środka ani brzegów. Pogląd ten został uznany przez Kartezjusza, Newtona i większość uczonych nowożytnych, dlatego dominował aż do połowy dziewiętnastego stulecia.

Wtedy to pojawiły się dwa paradoksy kosmologiczne, które podważały pogląd Bruno. Były to:

• (1) paradoks fotometryczny (świetlny) oraz
• (2) paradoks grawitacyjny.

Paradoks fotometryczny, sformułowany przez Heinricha Olbersa, głosi, że jeśli Wszechświat jest nieskończony i zarazem jednorodny (tzn. gęstość materii jest w dużej skali jednakowa – gwiazdy są równomiernie rozmieszczone), to całe niebo powinno w nocy jasno świecić. Z obserwacji wiemy, że niebo w nocy jest ciemne.

Paradoks grawitacyjny głosi, że jeśli słuszne jest prawo powszechnej grawitacji Newtona, to w modelu Bruno na dowolne ciało niebieskie, np. na Ziemię, powinny działać nieskończone siły grawitacyjne, idące od nieskończonych mas Wszechświata. W tej sytuacji powinien wystąpić tzw. chaos grawitacyjny, gdyż poszczególne ciała w pobliżu Słońca nie uwzględniałyby w swym ruchu skończonej siły przyciągania Słońca, która wobec nieskończonych sił materii Wszechświata byłaby nieskończenie mała.

Interesujące rozwiązanie obu paradoksów zaproponował szwedzki uczony Carl Charlier, który opracował hierarchiczny model budowy Wszechświata. Zgodnie z tym modelem gwiazdy skupiają się w gromady, tworząc galaktyki; galaktyki tworzą większe gromady (metagalaktyki) i tak w nieskończoność.

Jeśli założyć, że między kolejnymi gromadami istnieją coraz większe obszary (prawie) pustej przestrzeni, to oba paradoksy zostają rozwiązane. Jednakże model Charlier okazał się nieprawdziwy, gdyż zakładał, że dla nieskończonego Wszechświata gęstość materii zmierza do zera. W rzeczywistości bowiem gęstość materii w dużej skali okazała się wszędzie w przybliżeniu jednakowa.

Obecnie oba paradoksy kosmologiczne rozwiązuje ustalony przez Edwina Hubble’a w 1929 r. fakt „ucieczki galaktyk”, czyli rozszerzania się Wszechświata, polegający na tym, że galaktyki oddalają się od siebie tym szybciej im dalej się znajdują.

c) stanowisko nauki współczesnej XX wiek

Od czasu Newtona pojawiły się trzy wielkie odkrycia, które skomplikowały problem materialnej i przestrzennej nieskończoności Wszechświata:

• (1) Odkrycie z zakresu matematyki – odkrycie geometrii nieeuklidesowej przez Łobaczewskiego i innych. Zrodziło ono pytanie: która geometria rządzi światem. Rozstrzygnięcie problemu czy Wszechświat jest materialnie i przestrzennie nieskończony zależy bowiem od geometrii.
• (2) Drugie odkrycie z zakresu fizyki to ustalenie przez Einsteina i innych, że próżnia absolutna nie istnieje, co podważyło koncepcję Newtona o absolutnym czasie i absolutnej przestrzeni.
• (3) Trzecie odkrycie, również natury fizycznej to wykazanie przez Ogólną Teorię Względności (OTW) Einsteina, że przestrzeń naszego świata – przynajmniej lokalnie, w najbliższym otoczeniu kosmicznym – jest przestrzenią zakrzywioną dodatnio, czyli przestrzenią Riemanna.

Geometria Riemanna odróżnia pojęcie nieskończoności przestrzeni od pojęcia nieograniczoności przestrzeni:

nieskończoność przestrzeni ≠ nieograniczoność przestrzeni

Ciąg dalszy w kolejnym wpisie: Czy świat jest nieskończony?